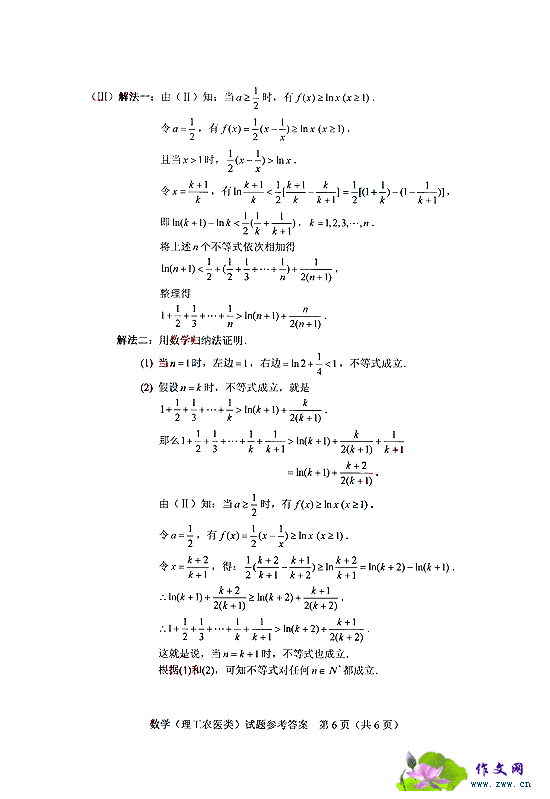2010年普通高等学校招生全国统一考试(湖北卷)
数学(理工农医类)
本试题卷共4页,三大题21小题。全卷满分150分。考试用时120分钟。
★祝考试顺利★
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。用2B铅笔将答题卡上试卷类型B后的方框涂黑。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。答在试题卷、草稿纸上无效。
3.填空题和解答题用0.5毫米黑色墨水签字笔将答案直接答在答题卡上对于应的答题区域内。答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的整洁。考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共10小题,每小题5分,共50 分,在每小题给出的四个选项中,只有一项是满足题目要求的。
1. 若i 为虚数单位,图中复平面内点Z表示复数z,则表示复数 的点是
的点是
 A. E B. F
A. E B. FC. G D. H
2. 设合集A={(x,y)|  +
+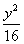 =1}, B={(x,y)|y=
=1}, B={(x,y)|y=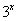 },则 B={(x,y)|y=
},则 B={(x,y)|y=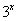 },
},  的子集的个数是
的子集的个数是
A. 4 B. 3 C. 2 D.1
3.在△ABC中, a =15, b=10 , A=60,则cosB=
A. -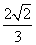 B.
B.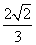 C.-
C.- D.
D.
4.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A,B中至少有一件发生的概率是
A. B.
B.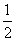 C.
C. D.
D.
5.已知△ABC和点M满足 +
+ +
+ = 0。若存在实数m使得
= 0。若存在实数m使得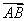 +
+ = m
= m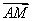 成立,则m=
成立,则m=
A. 2 B. 3 C. 4 D. 5
6. 将参加夏令营的600名学生编号为:001,002…600。采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003。这600名学生分住在三个营区,从001到300在第I营区,从301到495在第II营区,从496到600在第III营区。三个营区被抽中的人数依次为
A.. 26,16,8 B. 25,17,8 C. 25,16,9 D. 24,17,9
7.如图,在半径为 的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设
的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设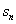 为前
为前 个圆的面积之和,则
个圆的面积之和,则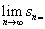
A..  B.
B. 


C. 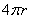 D.
D. 
8.现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每个从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加。甲、乙不会开车但能从事业其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是
A.152 B.126 C.90 D.54
9.若直线 与曲线
与曲线 有公共点,则b的取值范围是
有公共点,则b的取值范围是
A..  B.
B. 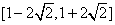
C.  D.
D. 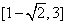
10.记实数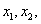 …
…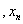 中的最大数为max{
中的最大数为max{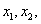 …
…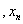 },最小数为min{
},最小数为min{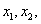 …
…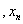 }.已知△
}.已知△ 的三边边长为
的三边边长为 (
( ),定义它的倾斜度为
),定义它的倾斜度为
则“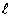 =1”是“△
=1”是“△ 为等边三角形“的
为等边三角形“的
A.必要而不充分的条件 B.充分而不必要的条件
C.充要条件 D.既不充分也不必要的条件
二、填空题:本大题共5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上,一题两空的题,其答案按先后次序填写.答错位置,书写不清,模棱两可均不得分.
11.在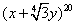 的展开式中,系数为有理数的项共有 项.
的展开式中,系数为有理数的项共有 项.
12.已知 ,式中变量
,式中变量 满足约束条件
满足约束条件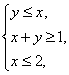 则
则 的最大值为 .
的最大值为 .
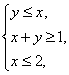 则
则13.圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示)。则球的半径是 cm。

14.某射手射击所得环数的分布列如下:
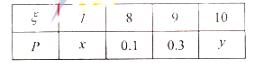
已知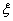 的期望
的期望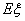 =8.9,则
=8.9,则 的值为 。
的值为 。
15.设 ,则
,则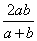 为
为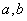 的调和平均数。如图,
的调和平均数。如图, 为线段
为线段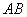 上的点,
上的点,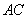 =
=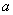 ,
, =
= ,O为
,O为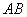 的中点,以AB为直径作半圆。过点
的中点,以AB为直径作半圆。过点 做
做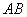 的垂线交半圆于D,连结
的垂线交半圆于D,连结 ,
, ,
, 。过点C做
。过点C做 的垂线,垂足为
的垂线,垂足为 。则图中线段
。则图中线段 的长度为
的长度为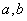 的算术平均数,线段 的长度是
的算术平均数,线段 的长度是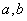 的几何平均数,线段 的长度是
的几何平均数,线段 的长度是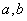 的调和平均数。
的调和平均数。

三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分12分)
已知函数f(x)=cos(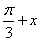 )cos(
)cos( ),g(x)=
),g(x)=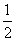 sin2x
sin2x
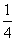 .
.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数h(x)=f(x) g(x)的最大值,并求使h(x)取得最大值的x的集合。
g(x)的最大值,并求使h(x)取得最大值的x的集合。
17.(本小题满分12分)
为了在夏季降温和冬季供暖时减少能源损耗,房屋的房顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用为C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0
(0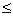 x
x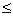 10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式;
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。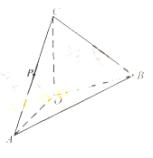

18.(本小题满分12分)
如图,在四面体ABOC中,OC OA,OC
OA,OC OB.
OB.
∠AOB=120,且OA=OB=OC=1
(Ⅰ)设P为AC的中点,证明:在AB上存在一点Q,使PQ OA,并计算
OA,并计算 的值。
的值。
(Ⅱ) 求二面角O-AC-B的平面角的余弦值。
19.(本小题满分12分)
已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有 若存在,求出m的取值范围;若不存在,请说明理由。
若存在,求出m的取值范围;若不存在,请说明理由。
20.(本小题满分13分)
已知数列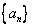 满足:
满足: ;数列
;数列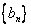 满足;
满足;
(Ⅰ)求数列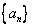 ,
,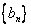 的通项公式;
的通项公式;
(Ⅱ)证明:数列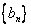 中的任意三项不可能成等差数列。
中的任意三项不可能成等差数列。
21.(本小题满分14分)
已知函数f(x)=ax+ +c(a>0)的图像在点(1,f(1))处的切线方程为y=x-1
+c(a>0)的图像在点(1,f(1))处的切线方程为y=x-1
(Ⅰ)用a表示出b,c;
(Ⅱ) 若f(x) Inx在
Inx在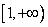 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;
(Ⅲ)证明: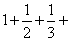 ……
……
参考答案